Skip to main content
Springer Nature Link
Log in

Approximation and Fast Calculation of Non-local Boundary Conditions for the Time-dependent Schrödinger Equation

  • Conference paper
Domain Decomposition Methods in Science and Engineering

Part of the book series: Lecture Notes in Computational Science and Engineering ((LNCSE,volume 40))

  • 1938 Accesses

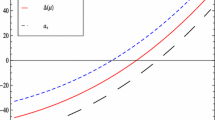
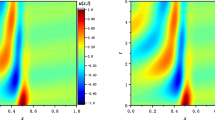
Summary

We present a way to efficiently treat the well-known transparent boundary conditions for the Schrödinger equation. Our approach is based on two ideas: firstly, to derive a discrete transparent boundary condition (DTBC) based on the Crank-Nicolson finite difference scheme for the governing equation. And, secondly, to approximate the discrete convolution kernel of DTBC by sum-of-exponentials for a rapid recursive calculation of the convolution. We illustrate the efficiency of the proposed method on several examples.

A much more detailed version of this article can be found in Arnold et al. [2003].

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  • A. Arnold. Numerically absorbing boundary conditions for quantum evolution equations. VLSI Design, 6:313–319, 1998.

    Google Scholar 

  • A. Arnold, M. Ehrhardt, and I. Sofronov. Discrete transparent boundary conditions for the Schrödinger equation: Fast calculation, approximation, and stability. Comm. Math. Sci., 1:501–556, 2003.

    MathSciNet  Google Scholar 

  • M. Ehrhardt and A. Arnold. Discrete transparent boundary conditions for the Schrödinger equation. Riv. Mat. Univ. Parma, 6:57–108, 2001.

    MathSciNet  Google Scholar 

  • I. Sofronov. Artificial boundary conditions of absolute transparency for twoand threedimensional external time-dependent scattering problems. Euro. J. Appl. Math., 9:561–588, 1998.

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institut für Numerische Mathematik, Universität Münster, Einsteinstr. 62, D-48149, Münster, Germany

    Anton Arnold

  2. Institut für Mathematik, Technische Universität Berlin, Str. des 17. Juni 136, D-10623, Berlin, Germany

    Matthias Ehrhardt

  3. Keldysh Institute of Applied Mathematics, Russian Academy of Sciences, Moscow, Russia

    Ivan Sofronov

Authors
  1. Anton Arnold
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Matthias Ehrhardt
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ivan Sofronov
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Moffett Field, CA

    Timothy J. Barth

  2. Bonn

    Michael Griebel

  3. New York

    David E. Keyes  & Tamar Schlick  & 

  4. Espoo

    Risto M. Nieminen

  5. Leuven

    Dirk Roose

  6. Fachbereich Mathematik und Informatik, Freie Universität Berlin, Arnimallee 2-6, 14195, Berlin, Germany

    Ralf Kornhuber

  7. Department of Mathematics, University of Houston, Philip G. Hoffman Hall 651, 77204-3008, Houston, TX, USA

    Ronald Hoppe

  8. Dassault Aviation, 78 Quai Marcel Dassault Cedex 300, 92552, St. Cloud, France

    Jacques Périaux

  9. Laboratoire Jacques-Louis Lions, Université Paris VI, 175 Rue de Chevaleret, 75013, Paris, France

    Olivier Pironneau

  10. Courant Institute of Mathematical Science, New York University, Mercer Street 251, 10012, New York, USA

    Olof Widlund

  11. Department of Mathematics Eberly College of Science, Pennsylvania Sate University, McAllister Building 218, 16802, University Park, PA, USA

    Jinchao Xu

Rights and permissions

Reprints and permissions

Copyright information

© 2005 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Arnold, A., Ehrhardt, M., Sofronov, I. (2005). Approximation and Fast Calculation of Non-local Boundary Conditions for the Time-dependent Schrödinger Equation. In: Barth, T.J., et al. Domain Decomposition Methods in Science and Engineering. Lecture Notes in Computational Science and Engineering, vol 40. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-26825-1_10

Download citation

Publish with us

Policies and ethics